Pada kesempatan kali ini, mari kita menjelajahi salah satu konsep yang menarik dalam geometri dan aljabar: kuadran. Apakah kalian penasaran tentang pengertian kuadran, bagaimana kita dapat mengidentifikasi mereka, dan bagaimana konsep ini dapat diterapkan dalam berbagai konteks? Jika ya, mari kita simak dan pahmi penjelasan dari konsep kuadran!
Pengertian Kuadran
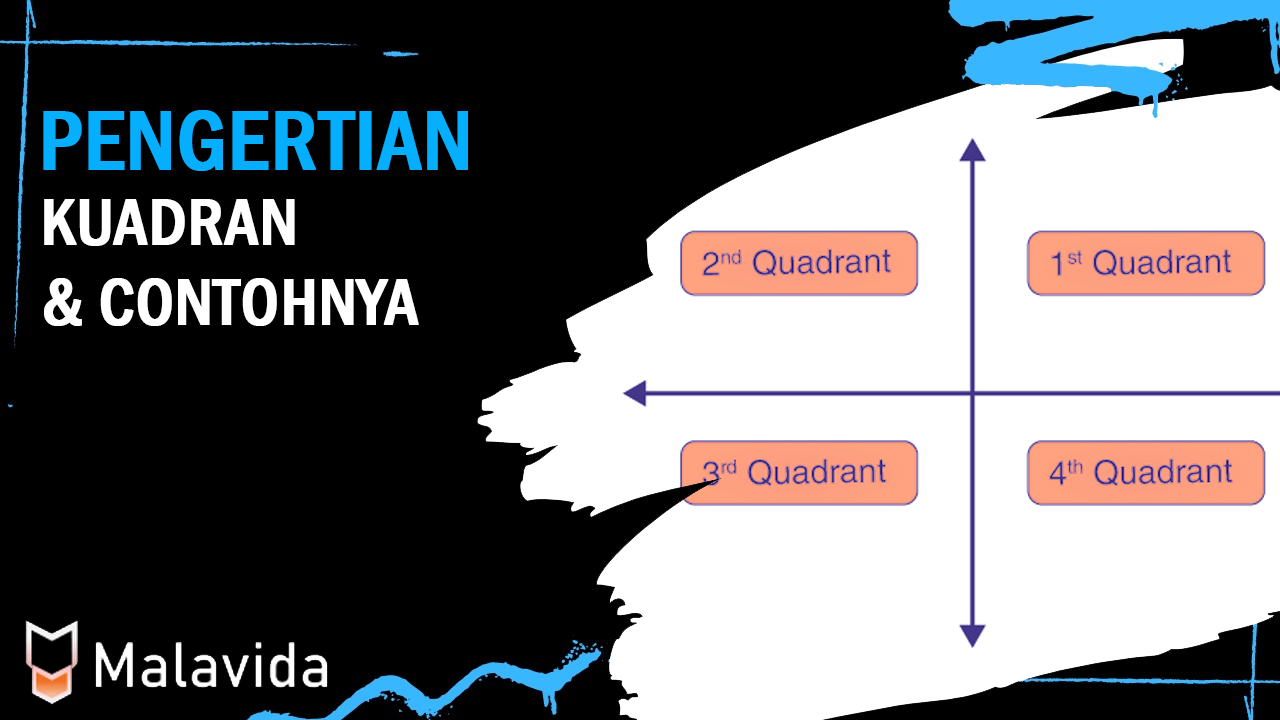
Sebelum kita membahas lebih jauh, mari kita definisikan terlebih dahulu apa yang dimaksud dengan kuadran dalam matematika
Kuadran:
Dalam geometri kartesian, bidang datar dibagi menjadi empat bagian yang sama besar oleh dua sumbu tegak lurus yang disebut sumbu-x (sumbu horizontal) dan sumbu-y (sumbu vertikal). Setiap bagian ini disebut kuadran. Kuadran diberi label sesuai dengan tanda-tanda koordinat titik-titik yang terletak di dalamnya.
Baca juga: Pengertian Kualitas dan Kuantitas serta Contohnya
Karakteristik Kuadran
Untuk memahami kuadran lebih baik, ada beberapa karakteristik penting yang perlu diperhatikan:
1. Pembagian Bidang:
Bidang datar dibagi menjadi empat kuadran yang sama besar oleh sumbu-x dan sumbu-y. Kuadran I terletak di kuadran kanan atas, Kuadran II di kuadran kiri atas, Kuadran III di kuadran kiri bawah, dan Kuadran IV di kuadran kanan bawah.
2. Label Koordinat:
Setiap kuadran diberi label sesuai dengan tanda-tanda (+) atau (-) dari koordinat titik-titik yang terletak di dalamnya. Kuadran I memiliki kedua koordinat positif (+, +), Kuadran II memiliki koordinat x negatif (-, +), Kuadran III memiliki kedua koordinat negatif (-, -), dan Kuadran IV memiliki koordinat y negatif (+, -).
3. Koordinat Khusus:
Di setiap kuadran, terdapat titik-titik yang memiliki koordinat khusus. Misalnya, titik (1, 1) terletak di Kuadran I, titik (-1, 1) terletak di Kuadran II, titik (-1, -1) terletak di Kuadran III, dan titik (1, -1) terletak di Kuadran IV.
Baca juga: Pengertian Kuadrat dan Contohnya
Contoh-contoh Kuadran dalam Kehidupan Sehari-hari
Sekarang, mari kita lihat beberapa contoh konkret tentang bagaimana konsep kuadran diterapkan dalam kehidupan sehari-hari:
Contoh 1: Navigasi
Kuadran digunakan dalam navigasi untuk menentukan arah atau posisi suatu objek atau titik. Misalnya, dalam peta atau sistem GPS, arah dapat ditentukan berdasarkan kuadran mana tempat tujuan berada.
Contoh 2: Grafik dan Diagram
Dalam statistik atau ilmu sosial, grafik dan diagram sering digunakan untuk memvisualisasikan data. Grafik kartesian dengan sumbu-x dan sumbu-y membagi bidang menjadi kuadran dan memungkinkan kita untuk mengevaluasi hubungan antara variabel-variabel yang berbeda.
Contoh 3: Analisis Keuangan
Dalam analisis keuangan, kuadran digunakan untuk mengelompokkan kinerja keuangan suatu perusahaan atau investasi. Misalnya, perusahaan yang memiliki pertumbuhan laba positif dan pertumbuhan pendapatan positif akan berada di Kuadran I, sementara perusahaan dengan pertumbuhan laba negatif dan pertumbuhan pendapatan positif akan berada di Kuadran II.
Contoh 4: Fisika
Dalam fisika, kuadran digunakan untuk menentukan arah dan posisi benda atau partikel dalam ruang. Vektor yang diarahkan ke kanan atas akan berada di Kuadran I, vektor yang diarahkan ke kiri atas akan berada di Kuadran II, dan seterusnya.
Kesimpulan
Kuadran adalah konsep yang penting dan bermanfaat dalam matematika, geometri, dan berbagai bidang ilmu lainnya. Dengan memahami karakteristik dan sifat-sifat kuadran, kita dapat mengenali pola-pola dan hubungan dalam berbagai konteks, mulai dari navigasi hingga analisis keuangan.




